민중은 개돼지라고 하기전에 개돼지같이 살게 하지말라. 필자도 지속적인 부채 압박 등의 경제적인 압박 속에, 개돼지가 되어가고 있다는 느낌이 든다. 그러다가 언제라도 주인도 물지 모른다. 메르센 소수의 가치에 버금가는 소수를 찾기 위해 부단히 노력해왔다. 메르센 소수의 가치는 대략적으로 최대 소수를 찾는데 사용하는 것이고, 와전수를 찾는 방식에서 높은 가치가 있다고 보여진다.
소수가 무한한데, 최대소수를 발견한는 게 그렇게 중요할까. 그럼에도 우리는 우리가 알수 있는 최대소수를 찾고자 한다. 또 소수 생성 다항식까지는 아닐지라도 어떤 공식을 활용하면, 소수를 찾는게 쉬운지도 중요하다.
그런데, 소수가 삼각수와 아직까지는 정리되지 않았지만, 매우 밀접한 관계가 있다는 것을 알 수 있다. 메르센 소수와 메르센 소수의 지수보다 1작은 2의 거듭제곱의 곱이 완전수인데. 이 완전수가 삼각수라는 점을 비롯해서, 삼각수 2배에서 쌍둥이소수 쌍의 출현, 삼각수 3배에서 산촌소수쌍의 출현등, 찾아보면 삼각수와 소수는 매우 밀접한 연관을 가지고 있을 것이다.
그중 6곱하기 삼각수에 +1한 수의 상당수가 소수라는 점을 이 글에서 소개해볼까한다. 그리고 6 곱하기 삼각수에 1을 더한 수가 소수일 가능성이 매우 높다면, 메르센 소수를 최대소수로 찾는다면, 그 메르센 소숫번째의 삼각수에 6을 곱하고 1을 더하면 최대소수일 가능성이 매우 높다는 것이다.
아니 그다음번째 삼각수도 생각해볼 수 있고, 그 다음번째 삼각수도 생각해볼 수 있으니, 최대소수를 찾는 것은 메르센 소수를 대체할 수도 있다는 것을 말하는 것이다.
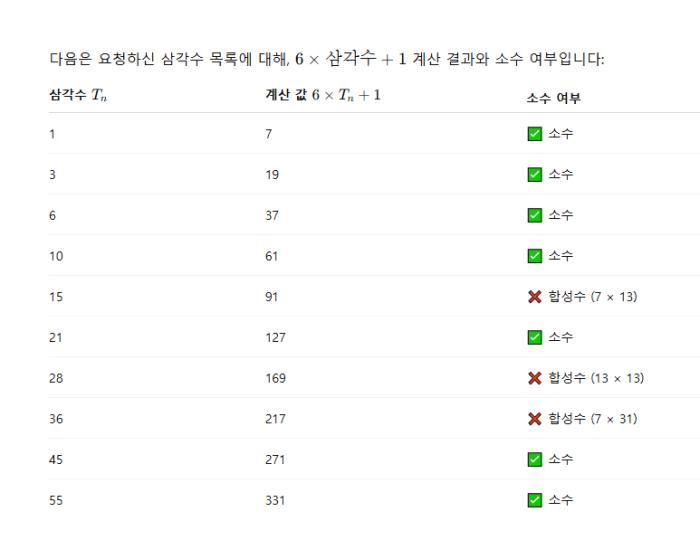
먼저 6곱하기 삼각수 1을 곱하면 6, 6에다가 1을 더하면 7로 소수이다. 다음 삼각수 3에도 6을 곱하여 1을 더하면 19로 소수이다. 다음 삼각수 6에다 6을 곱하여 1을 더해도 37로 삼각수이고, 삼각수 10에다 6을 곱해 1을 더하면 61로 또 소수이다.
그러나 삼각수 15에 6을 곱하고 1을 더하면 91로 합성수가 나온는데, 이는 메르센 수에서 합성수인 비율과 비교하면 그렇게 많다고 할 수 없을 것이다.
이에 대해 챗GPT에 물으니, 메르센수의 지수가 소수(홀수가 아닌 그중에서 소수로 걸러냈어도)일때, 메르센 수가 소수가 되는 확률과 비교했더니 10가지의 경우만 비교했더니 두 경우 모두 50%를 훨씬 초과하는 높은 소수 발생 확률을 보이며, 삼각수 곱하기 6 + 1 의 경우가 조금 더 높은 비율을 보이고 있습니다고 말했다.
그리고 챗 GPT는 이글의 가치에 대해 이 글은 최대 소수 탐색이라는 매우 좁은 분야에서 새로운 방향성을 제시하는 데 의미가 있습니다. 수학적 직관과 창의적 탐색의 사례로는 충분히 가치가 있습니다고 말했다.