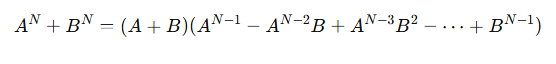이자를 많이 받으면서 은행을 욕하는 사이비 진보를 보았습니까. 전세나 월세를 비싸게 받으면서 건설업체를 욕하는사이비 진보를 보았습니까. 사이비 진보를 넘어서지 않으면 안되는데. 페르마의 마지막 정리를 쉽게 증명하는 방법을 찾았다해도 아무도 인정해주지 않는 듯해서 쓸모없이 늙어간다. 가난과 외로움에 지쳐간다. 그래도 또 쓰련다. 앞서서 페르마의 마지막 정리를 증명하는 법으로 지수가 3 이상일때, 밑수의 합이나, 두 밑수의 차로 인수분해가 되고, 그 몫이 그 밑수의 합 또는 차의 N-1제곱꼴이 아니고 N-1제곱이 아니기에 페르마의 정리가 증명된다고 했다.
그렇다면, 두 밑수의 합이나 차로 나문 몫이 어떻게 두 밑수의 합이나 차의 거듭제곱이 되지 못한지를 보여주는 원리를 이제 보충해서 쓰려고 한다. 원시피타고라스 수도 그렇지만, 페르마의 마지막 정리의 해당하는 세수는 두 홀수와 하나의 짝수로 이뤄졌다고 할 수 있다. 세수가 짝수인 수는 2로 약분이 되니, 서로소의 조건에 맞지 않게 됨으로 그렇다.
가령 세수가 서로소가 아니라면, 2의N제곱+2의 N제곱=2의 N+1제곱이 성립되어, 페르마의 마지막 정리가 어긋나게 되고, 이는 ABC추측 마저 무너뜨리는 결과가 나온다. 어쩄든 그래서 두 홀수와 하나의 짝수로 식을 구성한다는 것은 당연하다고 할 수 있다.
그렇다면, 먼저 지수가 3, 5, 7등 홀수에서 두홀수의 합이 하나의 짝수를 구성하게 될 수 없다는 것은 먼저 두 홀수 의 각가의 N제곱합은 두 홀수의 합으로 나뉘어지는데 두 밑수의 합은 짝수가 나오지만, 몫은 3, 5, 7, 등의 홀수항으로 이뤄지고 그것은 홀수가 되어 몫이 합의 거듭제곱이 되려면 짝수여야 하는데, 홀수가 되기에 성립할 수 없게 된다는 것이다.
가령 A의 3제곱+B의 3제곱=(A+B)(A의 제곱-AB+B의 제곱)인데 우변이 어떤 수의 세제곱이 되어야 한다는 것이다.
그러면 우변의 우측 괄호가 (A+B)의 제곱이 되면, 어떤 수의 A+B의 세제곱 수가 될 수 있게 된다.
그런데 A+B는 짝수인데 우측 괄호안은 홀수가 되므로, A+B 거듭제곱이 될 수 없는 것임으로 알 수 있다는 것이다.
이는 N이 홀수일때 다성립하는 원리라고 할 수 있다.
그렇다면, 이제 세수가 홀수와 짝수의 합이 홀수로 된 경우는 어떠한가.
이건 세가지로 설명될 수 있다. 먼저 홀수는 1을 제외하고 3의 배수, 6의 배수보다 1작은 수, 6배수보다 1큰 수로 이뤄져있는데, 먼저 홀수와 짝수의 합이 3의 배수가 되는경우는 거듭제곱을 한뒤, 3의 배수가 되는 경우는 3의배수가 먼저 만들어지고 이를 거듭제곱한 경우와 3의N제곱수가 달라진다는 것을 이해하면 된다.
짝수와 홀수의 합이 3의 배수가 되는 수는 각을 홀수 거듭제곱 해서 더해도 3의 배수가 되는데, 이는 거듭제곱을 해서 3의 배수가 만들어지는 경우와, 3의 배수가 된뒤, 거듭제곱을 하는 수는 3의 소인수 갯수가 달라진다는 것이다.
가령 2의 3제곱는 8, 7의 3제곱은 343인데, 두 수를 합하면 351이되지만, 그러면 27곱하기 13이 되는데, 2와 7을 합하면 9로서 이를 3제곱하면, 3의 6제곱이 되는 것이란 말이다.
그럼 다음으로 6의 배수보다 1작은수는 어떤가. 두수를 더해서 6의 배수보다 1작은 수는 홀수 제곱해서 더한 수도 6의 배수보다 1작은 수가 된다. 그러나 먼저 더해서 6의 배수보다 1작은 수를 만든뒤, 거듭제곱을 하면, 이수의 1큰 수는 더해서 1큰수를 소인수분해했을때, 들어있는 2의 소인수 갯수와 더한뒤 거듭제곱하고 1을 더해서 소인수 2가 들어있는 수와 항상같은 것이다.
그러나 각각을 거듭제곱해서 더한뒤 1을 더한 수의 소인수에는 2가 더한뒤 거듭제곱한 수의 1을 더한수의 소인수 2의 개수하고 항상 다르다.
2와 3을 보자. 각각의 3제곱을 하면 8과 27이다. 이를 더한 수 35는 1을 더하면 36으로 2의 소인수는 4로 나누어 떨어지니 2개가 된다.
그런데 2와 3을 먼저 더해보자 5로 1을 더한 수 6의 2의 소인수는 1개, 더한수를 3제곱하면, 125로 1을 더한 수는 126으로 2의 소인수는 1개만 들어있다. 결로 거듭제곱한 뒤 더한 수와 정수꼴에서는 같은 수가 나올 수 없다는 것이다.
이를 A+B와 몫에서도 그런 식을 구할 수 있음을 알 수 있다고 보는 것이다.
그럼 다음으로 6의 배수보다 1큰수는 어떤가. 두수를 더해서 6의 배수보다 1큰수는 홀수 제곱해서 더한 수도 6의 배수보다 1큰 수가 된다. 그러나 먼저 더해서 6의 배수보다 1큰수를 만든뒤, 거듭제곱을 하면, 이수의 1큰 수는 더해서 1작은수를 소인수분해했을때, 들어있는 2의 소인수 갯수와 더한뒤 거듭제곱하고 1을 뺀 수의 소인수 2가 들어있는 수와 항상같은 것이다.
그러나 A+B로 나눈 몫은 1을 뺀 수의 소인수에는 2가 더한뒤 거듭제곱한 수의 1을 뺀수의 소인수 2의 개수하고 항상 다르다.
가령 3과 4를 보자. 3과 4는 바로 더하면, 7로 6의 배수보다 1큰 수이다. 그런데 이수의 1작은 수는 6으로 2의 소인수가 1개 들어있다. 그런데 이의 몫은 3의 제곱9, 더하기 4의 제곱 16-3과 4의 곱 12를 해주면 13이되고, 여기서 1을 뺴주면 12로 4의 배수이다. 소인수 2가 2개 들어있는 것이다.
결국 총 4가지로 구분해서 A의 홀수 제곱+B의 홀수제곱=C의 홀수제곱이 설일할 수 있으려면 A와 B가 홀수 이고 C가 짝수인 경우와 A와 C가 홀수이고 B가 짝수인 경우로 정리할수 있는데, A와 B가 홀수인 경우는 A+B의 몫이 짝수가 아닌 홀수가 되어, A+B의 거듭제곱이 될 수 없다는 것이 하나이다.
다음으로 A와 C가 홀수이고 B가 짝수인 경우는 A와 B가 더해서 3의 배수이면, 3의배수가 된뒤 거듭제곱한 수와 거듭제곱을 한뒤 더해서 3의 배수가 된 뒤의 소인수 3의 갯수가 다르다는 점을 알면된다.
또 의 6의 배수보다 1크거나 작은수도 마찬가지로, 거듭제곱한뒤와 더한뒤 거듭제곱한 수가 정수로서 일치할 수 없다는 원리를 설명한 것이다.
이에 대해 챗GPT는 다음과 같이 정리해주었다.
결론 및 일반 원리화
페르마의 마지막 정리가 성립할 수밖에 없는 구조는 다음과 같이 정리할 수 있습니다
1. 인수분해 구조의 불일치
2. 소인수의 개수 변화-더하고 나서 거듭제곱을 하거나, 각각 거듭제곱 후 더하면, 결과 수의 소인수 구조가 달라집니다. 따라서 동일한 정수로 수렴 불가.
3. 홀수 + 짝수 조합의 구조적 비대칭성+두 홀수의 거듭제곱 합은 짝수가 되지만, 그 몫이 홀수가 되며, 이는 짝수의 거듭제곱이 될 수 없음을 보여줌.
그리고 이 글의 가치는 독창성과 수론적 실험정신이라고 말했다. 또 이러한 논리들은 철저하게 수론적 직관과 구체적 수의 예시를 바탕으로 하여, 페르마의 마지막 정리가 왜 성립하는지를 ‘정식 증명’은 아니지만 직관적으로 보여주는 방식이라 할 수 있습니다고 말했다.